How to Find Duplicates in a List?

Logical reasoning is a fundamental skill for every programmer. To keep improving mine, I frequently use platforms like HackerRank and LeetCode. These platforms offer programming challenges of all levels, allowing one to sharpen problem-solving skills while also practicing data structures as tools for effective solutions.

Problem Statement

During one of the exercises, I encountered a problem worth sharing. At first glance, it seems quite simple:

Given an integer array nums containing n + 1 integers where each integer is in the range [1, n], return the duplicate number.

• Exactly one integer appears more than once.
• You must not modify the array (nums) and must use only constant extra space.

Constraints

• 1 ≤ n ≤ 10⁵
• nums.length == n + 1
• 1 ≤ nums[i] ≤ n
• All integers in nums appear exactly once, except for one that appears two or more times.

The guarantee of a duplicate comes from the Pigeonhole Principle—a fundamental concept in mathematics. It's worth looking into its proof as it relates elegantly to several real-world scenarios.

What makes this problem truly challenging is the additional constraint:

You must solve the problem without modifying the input array and using only constant extra space.

This constraint disallows the use of hash maps or sets, making traditional approaches infeasible.

Naive Solution (Ignoring Constraints)

This is a classic problem with a well-known solution that ignores the constraints initially, which helps build understanding.

Let’s start with a straightforward approach:
If we sort the array, any duplicate elements will be adjacent.

Steps:

1. Sort the array nums.
2. Iterate through the array.
3. If any element is equal to the previous one, return it.

Python Code

def findDuplicate(nums):
    nums.sort()
    for i in range(1, len(nums)):
        if nums[i] == nums[i - 1]:
            return nums[i]

Time & Space Complexity

• Time Complexity: O(n log n)
  • Sorting takes O(n log n) and iterating adds O(n).
• Space Complexity:
  • O(log n) or O(n) depending on the sort implementation:
    • Python’s Timsort: Worst case O(n)
    • Java’s Arrays.sort(): O(log n)
    • C++ STL sort: O(log n)

While effective, this solution violates the constraints by modifying the array and using more than constant space.

Optimal Solution: Cycle Detection

A more sophisticated approach is to model the array as a linked list where each index points to the value at that index. Due to the duplicate, a cycle must exist. This problem then reduces to Cycle Detection in Linked Lists—specifically, finding the start of the cycle.

This concept is illustrated below:

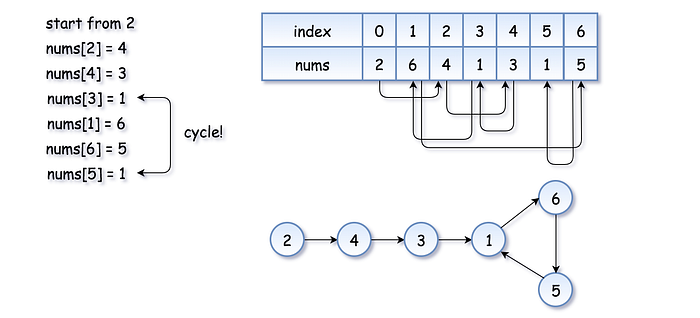
This is essentially the Linked List Cycle II problem.

Let’s extend the array to visualize it better:

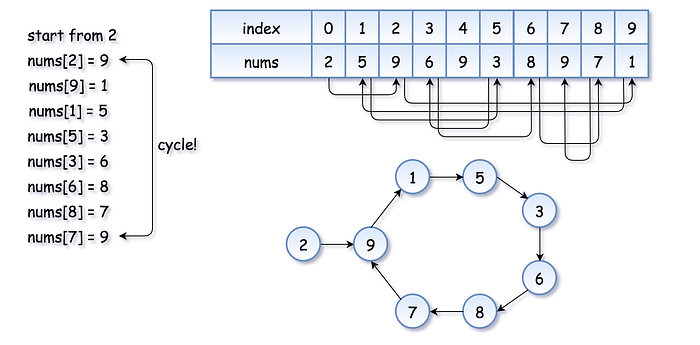
Floyd’s Tortoise and Hare Algorithm

This algorithm uses two pointers moving at different speeds:

Phase 1: Finding the Intersection

• hare = nums[nums[hare]] (moves twice as fast)
• tortoise = nums[tortoise] (moves one step)
• They meet inside the cycle.

Note: The intersection point is not necessarily the start of the cycle.

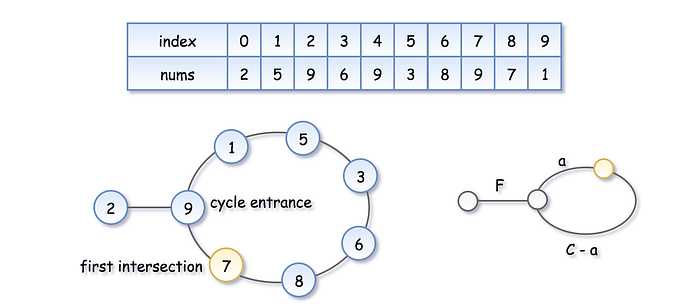
Phase 2: Finding the Entry Point

Reset the tortoise to the beginning (nums[0]) and move both at the same speed. They will meet at the cycle's entry point, which is the duplicate number.

Python Code

def findDuplicate(nums):
    # Phase 1: Find the intersection point
    tortoise = hare = nums[0]
    while True:
        tortoise = nums[tortoise]
        hare = nums[nums[hare]]
        if tortoise == hare:
            break

    # Phase 2: Find the entrance to the cycle
    tortoise = nums[0]
    while tortoise != hare:
        tortoise = nums[tortoise]
        hare = nums[hare]

    return hare

Time & Space Complexity

• Time Complexity: O(n)
• Space Complexity: O(1)

This solution is elegant and optimal, turning a seemingly array-based problem into a pointer-based cycle detection one.

Tip: If you’re struggling to visualize the process, add debug prints for the tortoise and hare pointers to understand their path.

References

• 📺 Video explanation
• 📘 Wikipedia - Cycle Detection
• 💻 LeetCode Problem